当企画について
(この記事は常にトップに表示されます)
公式ホームページはこちら
【本企画について】
「PhysicsLab. 2017」は東京大学理学部物理学科の学生有志による展示企画です。
東京大学の学園祭、「五月祭」にて物理に関連した展示や講演、実験ショーを行います。五月祭当日は是非本郷キャンパス理学部1号館へお越しください。
今回の企画では低温班・計算機班・シンクロ班・量子測定班・宇宙班・スピン班・実験ショー班の7つの班が結成され、一年近く準備をしてまいりました。各班の研究成果を通して物理に楽しく触れていただける企画を準備しています。
物理なんて全然分からないという方でも大丈夫。どんな方にも感動を味わっていただくべく、至る所に工夫を施しています。
せっかくの五月祭、ここ本郷でちょっと心くすぐられる、そんな感動を体験してみませんか?
【開催日時】
2017年 5月20日(土)・21日(日)
両日とも 午前9時〜午後6時
メトロノームを物理の世界から見ると
シンクロ班の宮崎と申します。
前回の記事では「振動子」と「同期」の簡単な説明をしたので、まずはそちらをご覧ください。
→ http://ut-physlab.hatenablog.jp/entry/2017/03/26/225014
今回はシンクロ班の目玉商品、メトロノームについてお話ししましょう!2つクイズを出すので皆さん考えてみてくださいね。

さて1つ目の問題です。なぜメトロノームは一定のリズムでチクタク振れるのでしょうか?普通なら摩擦によってだんだん減衰するはずですが...
答えは、メトロノームの内部には針をキックする装置が入っていて、それが減衰分を補っているからです。
続いて2つ目の問題です。静止した状態でそこから思いっきり針を振った時も、ちょっとしか針を振らなかった時も、ある程度時間が経てばどちらも一定幅での振動に落ち着きます。言い方を変えれば、どんな始状態でも同じ終状態に至るということです。これはどうしてでしょうか?
針の動きには摩擦とキックが関係していることに気づけば解決します。振れ幅が大きい時は摩擦が強いため減衰していきますが、逆に振れ幅が小さい時はキックが勝つのでもっと大きく揺れようとします。振れ幅一定というのは、この摩擦とキックがちょうど拮抗する所なのですね。この最終的に行き着く所を「リミットサイクル」と呼びます。
次は図で理解してみましょう。

横軸が針の位置、縦軸が針の速度です。(正確には速度ではなくて運動量です。)最初は赤い四角の状態からスタートして、矢印方向に移動していき、最終的にはずっと同じ軌道をぐるぐる回っていますね。これは、初め振れ幅が大きい状態で手を離すと、ある程度振動を繰り返した後、一定幅で振れる状態へと収束することに対応します。この収束先がリミットサイクルです。
今回はリミットサイクルに焦点を当ててお話ししました。五月祭当日(20、21日)は詳しい説明と共に、たくさんの実験をお見せしようと思います。fぜひ理学部1号館に足を運んでいただき、楽しい物理の世界を味わってください!
(これより先はちょっと難しいことを書くので、物理に興味のある方は読んでみてください。)

ここまでお読みいただきありがとうございます。理学部物理学科は五月祭で皆さんが来ていただけるのを心よりお待ちしております。
100年前のある発見について
最近、結膜炎になってしまって大変です。けっこう落ち込んでいます。
ではでは始めます……
突然ですが、みなさんははく検電器というシロモノをご存知でしょうか。知らないと思います。これがけっこう大事な話なので、説明します!
金属の小さくて薄いペラペラ(金属はく)が二枚だけ先端についた金属棒を、金属のふたがついている瓶の中に吊るします。つるし方は、はくが付いていない方の金属棒の端をふたにくっつけるだけです。こうしてできあがったのがはく検電器です。これだけです。
要はびんのなかに金属のぴらぴらが二枚ぶら下がってるだけです。
まわりくどい説明をするより見せたほうが早いとぼくも思うのですが、画像掲載の仕方がわからないので、いまこれを読んでいるスマホかパソコンで調べてみてください。いやはや、手間をかけさせて申し訳ありません。
気になるのは、このはく検電器はなにに使うのかということです。その前に少し電気の説明をします。
電気にはプラスとマイナスの二種類があります。それに伴い、電気を帯びた物質(電荷)も、その帯びている電気がプラスなのかマイナスなのかで二種類に分類できます。プラスの物質を正電荷、マイナスの物質を負電荷と言います。
想像がつくと思いますが、プラスを帯びた物質(正電荷)同士やマイナスを帯びた物質(負電荷)同士は反発しあい、正電荷と負電荷は引き合います。電気や磁力によって物質にはたらく効果を「電磁相互作用」なんて呼びますが、反発したり引き合ったりというのは電磁相互作用の一部なのです。
さて、はく検電器に戻りましょう。はく検電器に正電荷だけを与えると、金属のぴらぴらにも正電荷だけが新たにたまっていきます。片方のぴらぴらにたまった正電荷は、もう一方のぴらぴらの正電荷と反発して、ぴらぴら同士が互いに離れます。
ぴら ぴら →[正電荷をたくさん与える]→ ++ぴら++ ++ぴら++
ということです。ちょっとこの図は意味がわかりづらいですが、ナンセンスで面白いので掲載しておきます。
はく検電器は要するに、電気の相互作用を目に見えるかたちにしてくれるのです。大切なことは、はく検電器に正か負かの電荷どちらかだけを送り込むと、ぴらぴらが離れるということです。
100年前、このはく検電器で実験をしている人がいました。
――実験をしていたのかは定かではないので、もしかしたら遊んでいたのかもしれませんね。ぴらぴらを眺めながら、「あ~正電荷同士が反発してる~」とか「ぴらぴらがひらいた~」とか言って遊ぶのでしょうか。非常に勝手な推測ですが、昔は今ほど娯楽もなかったのでしょう。ですから、ぴらぴらを眺めているのはとても高級で洒脱な暇つぶしだったのではないでしょうか。「今日、ぴらぴらで遊ばない?」なんて。これはさすがに適当を言いすぎですかね。冗談ですよ。まあ、おそらく実験していたのでしょう――
その人は正電荷をはく検電器にためて、ぴらぴらが離れている状態にし、それを放置しておいたのです。すると、どうしたことでしょうか。少し長い時間が経つと、ぴらぴらの離れ具合が減少しているのです。あれれ、昨日より近づいていないか?という具合に。時間がたてばたつほど、ぴらぴらは互いの距離を詰めていきます。
すこしちゃんと考えてみましょう。ぴらぴら同士が近づくとはどういうことでしょうか。
ぴらぴらの位置が変わったのですから、ぴらぴらにかかる力になにか変化があったのでしょう。
ぴらぴらにかかる力は、重力と電気の力の二種類しかありません。風などからも、びんに守られています。
重力は変化しないでしょうから、電気の力の大きさが変化したということでしょう。
ぴらぴらにかかる電気の力の大きさは、「ぴらぴらにたまっている電気の量」と「ぴらぴら同士の距離」で決まります。
いまは、力の大きさが変化することで初めて距離が変わったのだと考えていますから、今回の力の大きさの変化は「距離の変化」に起因するのでなく、「電気の量の変化」に起因しているはずです。
でもどうしてそんなことが起こるのか。実は、昔の人たちはこの疑問についてはあまり悩みませんでした。彼らは、空気中で正電荷や負電荷がつくりだされることを知っていたからです。
地球の地面や建物の材料からは、ガンマ線など、少しだけ高いエネルギーをもつものが常に微妙に放出されています。これらは自然放射線の一種です。こういった自然放射線によって、空気中の原子はプラスとマイナスとに切り離される――電気的に分離するということでこれを「電離」と呼びます――ことがあるのです。勢いの良いビームによって、原子中の電子が飛んでいくイメージでよいです。これを昔の人たちは知っていましたから、はく検電器の件についてはそんなに驚愕というわけではなかったでしょう。
さて、歴史が動いていくのはここからです。すいません、お待たせして。
地面から出る放射線が、ぴらぴら接近のもともとの原因でしたから、エッフェル塔の頂上なんてところに行けば、接近具合は減少するのではないかと予測できます。高度があがればあがるほど、空気の電離レベルは下がり、はく検電器の電荷は消費されない。
ところが、実験結果は正反対でした。より高い場所では、ぴらぴらはより早く、接近するのです。すなわち、空気の電離レベルは高度上昇に伴って上昇する。えらいことです。
「上空の空気のほうが電離している!?これじゃあ、まるで勢いのあるビームが空から降ってきているみたいじゃないか!」
空から降ってくる謎のエネルギー。そう、これがまさに宇宙線発見の瞬間でした。
モデル化
こんにちは、計算機班です。
前回は計算機が物理でどう役立っているのかを見ていきました。
そこでは計算機の計算力でもって物理を紐解いていくということをお話ししましたが、「紐解くと言っても具体的にどんなことをするのか?」「じゃあ、頑張るのはコンピュータであって物理学者じゃないのかよ」とかいう某SNSの某ゴリラに襲いかかられそうな質問が生じるのが当然かと思いますので今回はその辺をお話ししようと思います。
長ったらしい説明の前に今回の話を一言で言うと「モデル化」です。
<物理現象のモデル化>
私たちの身の回りの物理現象は、様々な物理量が様々な物理法則のもとで変化した、または変化しないその結果です。したがって注目する物理量がどう変化するのか計算したい時に、どんな物理法則があるのかということを計算機に教えてあげないと計算機は計算を始められません。
とはいえ、たくさんある物理法則のうちで物理量の変化に影響を及ぼさない法則があることも事実で、こういった法則は無視してもよさそうですよね。無視したほうが計算量が減るので計算スピードが上がるので無視できるものは無視するのが賢明です。また、たくさんあるうちの物理法則の中には私たちがまだ知らない法則があるかもしれません。こういった法則に対しては、観測や理論から打ち出された法則の「候補」を使ってやるのが妥当です。
このように対象とする物理現象を、計算が収束するように単純化したり、「候補」を考えることを「モデル化」と言います。
単純化すればいいとは言いましたが、単純化にも限度があって、あまりに単純化しすぎると現実の物理を十分に再現できなくなってしまうのでどの程度までのモデル化が十分かつ必要か見極める必要があります。
また「候補」探しには、先行研究をよく知っておく必要があります。ある一つの「候補」での計算結果が、他の観測や理論と一致しないならその「候補」がハズレだったということで次の「候補」探しの手がかりにします。
物理現象のモデル化に物理学者の仕事の一つがあります。
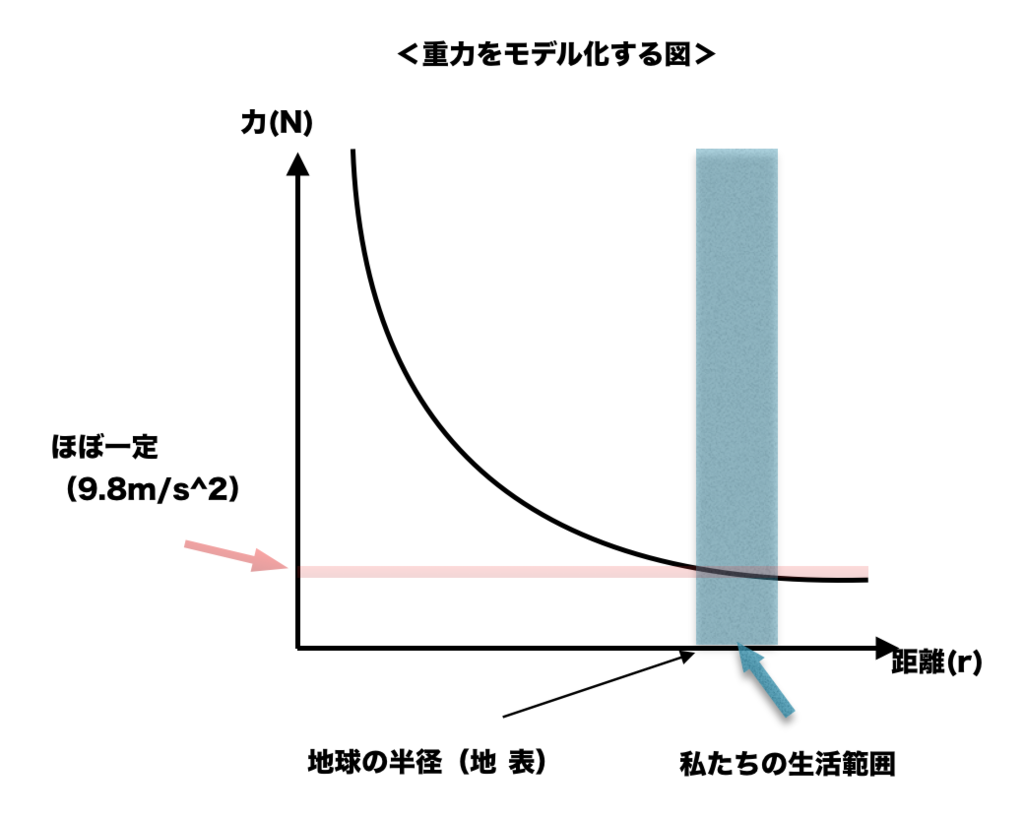
あまりピンとこない人は具体的に重力のモデル化を考えてみましょう。
重力の大きさは、私たちが地球の中心から距離r離れたところにいた時にrの二乗に反比例します。
しかし実際地球に住んでいる限りは地球からそんなに遠く離れないので先ほどのrはほとんど地球の半径と見なせます、つまり受ける力の大きさは反比例せずほぼ一定です。これがご存知重力加速度g=9.8m/s^2ですね。
今のような「私たちの(垂直方向)移動範囲は地球の大きさに比べたら小さいから重力はほぼ一定とみなしていいでしょ」がモデル化です。
<計算モデルの選択>
物理現象のモデル化を先ほど話しましたが、計算物理学に於いては「計算モデル」を選ぶという、これまたエッセンシャルな仕事があります。
物理の方程式には微分がたくさん登場するのでひとまず微分を考えてみましょう。
計算機は数値計算をするので、私たちが扱う微分積分を差分和分に置き換えて計算します。
微分積分は差分和分の極限でありますが、ある微分積分に対応する差分和分は一意(一通り)ではありません。
具体的に言うと微分
に対応する差分は(代表的なもので)
が考えられます。これらだけを見ても3通り、さらにΔxの取り方には無限の取り方があります。
3通りの選び方によって計算結果はだいぶ変わってきます。Δxは元の微分を保ちたいのだから小さいほうが良さそうですが実は小さく取れば良いってものでもないのです。これらを選ぶにはどの差分和分が考えている物理現象に即した考え方になっているか、とか、たくさん計算した時に最終的に得られる計算結果が発散せず欲しい精度に収まるようなΔxはどれぐらいか、という考察をしてからプログラムしないとなりません。
たった一つの微分でもこれだけの考察があります。
実際に考えるのは、より高階の微分が含まれている微分方程式だったり、めちゃめちゃでかい行列計算だったりするので、欲しい精度や性質を保つように、適切な計算方法を選んでいく必要があります。
計算モデルの選択(既存の計算モデルで対応できなければ作るわけですが)に物理学者のもう一つの仕事があります。
だいぶ浅くモデル化を見ていきましたが、モデルの面白さは各モデルを深く掘り下げていったその先にあるので是非五月祭に足をお運びください。
来て!見て!!わかる!!!超流動のフシギ
こんにちは、低温班の粂です。
前回の記事では班長の垂水くんがヘリウムの性質についてのお話をしてくれました。それによるとヘリウムが液体になるためには、なんと-269℃まで冷やさないといけないのですが...
僕たちの実験では液体のヘリウムをさらに冷却する
ことで見られる不思議な現象、『超流動』の様子・性質を動画に撮影しています!
『超流動』、聞きなれない言葉ですよね。でも実は
そんなに難しい話じゃありません。
案外文字通りなんです。超、流れるんです。液体ヘリウムを冷やすと、めちゃくちゃ流れるようになっちゃうんです!Σ( ; ゜Д゜)
少し具体的な話をしましょう。液体には「粘性」というものがあります。要は「ネバネバ度」です。
液体のりとかハチミツは「粘性」が高く、どろ~んとしています。容器を逆さまにしてもなかなか流れてこない、みなさんも経験ありますよね?それに比べると水はなめらかに流れているように感じます。ですが、それでもある程度の「粘性」を持っていてゼロではありません。
ここまで来ると察しの良い方は分かったかもしれませんね(笑)。そうなんです、液体ヘリウムを冷やして『超流動』状態にすると、「粘性」がゼロになってしまうのです!!
...え、いまいちスゴさが分からない??
ですよね。僕も実験して様子をこの目で見るまではピンと来てませんでしたf(^^;(笑)
それもそのはず。皆さんが「日常生活で目にする液体」には粘性があるわけですから、「粘性がゼロになった液体がどんな様子なのか」なんて全く想像もつかないはずです。
ですが逆手にとれば、「『超流動』になった液体ヘリウムは『非日常的』な振る舞いを示す」と言うこともできるでしょう。ちょっと格好つけちゃいましたがホントのことなのです!
「コップに水を注ぐと水が溜まっていく」、日常では当たり前のこんなことを『超流動の液体ヘリウム』でやると一体どうなると思いますか...???
...と、いうことで僕たちの実験では『非日常的な振る舞い』を皆さんに分かりやすく見てもらえるような工夫が施されています。『視覚的に楽しめる実験』になっていますので、実験結果(撮影した動画)も皆さんの興味を惹き付けること間違いなしです!!
超流動状態になったヘリウムの超日常的な振る舞い、そして僕らがそれをどのように検証したのか、一体どんな動画を見ることができるのか。
気になった方は是非、低温班のブースに遊びに来てください!!きっと皆さんの想像の斜め上を行くような実験結果が待ち受けているでしょう( ^∀^)

おまけ ~超流動と超伝導~
みなさんもしかしたら『超伝導』は聞いたことあるんじゃないでしょうか??よくリニアモーターカーの話なんかと一緒に出てくると思います。
物体を冷やしていくとある温度を境に「電気抵抗」が消失する、というやつです。
...あれ、なんか超流動と似てませんか??
物体を冷やしていくとある温度を境に「粘性」が消失する、これが超流動です。
実はこの2つの現象、どちらもBEC(ボーズ・アインシュタイン凝縮)の結果として現れていると考えられています!
僕たちは去年はBEC班として活動していました。BECは「ミクロな世界(量子力学)」と「マクロな世界(熱力学)」を結びつける「統計力学」によって予言された現象です。
超伝導と超流動、これら2つの異なる現象の背景にあるBEC。詳しいことが気になった方は低温班の班員に質問してみてくださいね!お待ちしてますo(^o^)o
long range article
こんにちは。電子スピン班班長の齊藤です。
4月も中旬になり、新生活が本格的に始まりましたね。
まだまだ三寒四温を感じる季節ですが、皆様におかれましてはいかがお過ごしでしょうか。
今週は電子スピン班から、明日からデカい顔して語れる物理をお送りしたいと思います。
テーマは「対称性とトポロジー」です。
Physics Lab.2017で電子スピンが展示する内容の一つに、「古典スピン系」があります。
これは、スピン同士に働く相互作用の効果で、配列されたスピンが特徴的な振る舞いをするというものです。
業界用語を出すと、Ising模型、XY模型におけるBKT転移、DM相互作用を取り込んで生じるskyrmion、です。
ちょっと何を言っているかわからない、という人のために、統計力学の補足説明をします(知っている人は読み飛ばしていただいて構いません)。
統計力学では、系(*1)のハミルトニアン(*2)によって、ある状態の実現する確率が分かる、と主張します。
確率Pはに比例します。大事なのは、エネルギーが小さいほど確率が高い、という点です。
古典スピン系のハミルトニアンと、ある状態が実現する確率は、スピンを使って
、
のように書け、この値を小さくするようにスピンの向きが決まります。
ただ、確率は温度にも依存するので、ある温度(転移温度)よりも低温か高温かで実現する状態が異なる場合があります。
大雑把には、温度が高いとエネルギーの違いによる効果が薄まるので、スピンはバラバラになります(このことはエントロピーを計算することでも言えます)。
さて、ここで「バラバラ」とはどういうことか考えてみましょう。
熱力学的には、エントロピー(*3)が大きいという言い方になります。
これを、対称性という観点から見ることもできます。
バラバラの反対は「揃っている」ですね。揃っているとは、つまりある種の対称性が破れているということ。
これは、下の絵を見てもらえば分かると思います。

左側は、矢印が上向きに揃っていて、明らかにこの方向だけ他の方向と違いますね。一方、右側は特にどの方向が特別ということもありません。
一般に対称性は、ある操作を施しても変わらない、というような操作によって定義されます。
上の絵の場合は、回転という操作に対する対称性の問題でした。次の絵は、先ほどの絵を時計回りに90度回転させたものです。

めっちゃ速く見比べて見てください。左は回転によって大きく変わっているのが分かります。
対称性が破れる、とは操作に対して不変でなくなる、すなわち系が指向性を持つということです。
何らかのパラメータを変化させていって対称性が破れた時、今まで現れていなかった性質が現れます。これを「相転移」と言います。
紙面の都合上、XY模型に話を絞ります。
XY模型はスピンが単位円上の任意の値を取れるのですが、これは2次元の回転に対して対称性を持つと言えます。
このような系では、スピンの配置の次数が2次元以下の場合、対称性の破れによる転移が生じないことが示されています。
そのため、XY模型では相転移が生じないものと思われていたのですが、実は違うタイプの相転移が生じると主張したのが、昨年のノーベル物理学賞に輝いたThoulessらです。
詳細は省きますが、転移温度以上では(仮想的な)欠陥をスピンが渦状に取り囲むような状態が安定となり、転移温度以下ではそのような渦が生じ得ないことが言えます。
さらに、この渦は連続的な(*4)変形によって渦でない状態に変えることができません。

このように「空間に穴があるか、無いか」を数学的に取り扱うのが「位相幾何学」という分野で、ホモトピーや代数ホモロジーという手法を駆使します。
物理の人は、これらをまとめてトポロジーと呼んでいます。
当初の予定よりもずいぶんたくさん書いてしまいました。
僕の嗜好の都合上、分かりにくく理屈っぽい説明になってしまったかもしれません。
知恵熱が出た人は、おでこに冷えピタ貼って、上に書いたことはとっとと忘れましょう。
ではでは、当日お会いできるのを心待ちにしております(_ _)
P.S.
twitterでは、電子スピン班の前回記事のskyrmionに対して反響が大きかったようですが、本物を見るのはあまりに大掛かり設備が必要なので、XY模型共々今回は計算機上でお見せします。ご了承ください。
>注釈
*1 考えている物理的対象のこと
*2 系のエネルギー(の意味を持つ演算子)
*3 で定められる量で、乱雑さの意味を持つ
*4 滑らかに、くらいの意味で捉えればよい
ショー班 ふりこのお話
こんにちは,ショー班です.
みなさんは,「ふりこ」をご存知でしょうか?
こんな感じで,おもりを糸につないだもののことです.

実はわざわざ作らなくても,身の回りにはたくさんの「ふりこ」があります.
たとえば,ブランコがそうです.

ふりこが「ゆれる」ことを使ったおもちゃですね.
他にも,干している洗濯物はふりこのようにゆらすことができます.
最初のふりこと見た目は違いますが,ふりこと同じように動きますね.
今日はそんなふりこに関するお話です.
さて,みなさんは次のようなことを聞いたことはありますか?
「ふりこが1回ゆれる時間は,ふりこのゆれ幅を大きくしても変わらない」
つまり,こんな感じです.

おもりが行って帰ってくるまでの時間は,どちらも同じです.
「初めて聞いた!」という人はちょっと驚いたのではないでしょうか.
暇なときに試してみると面白いですよ.
一方,「聞いたことあるよ」という人もいますよね.
その人にぜひ考えてみてほしい問題があります.
ふりこのゆれ幅をもっと大きくします.すると,おもりの位置も上がっていきます.

糸を使うとたるんでしまうので,物干し用のハンガーを使ってみましょう.
ハンガーを持って,真上を向かせます.

完全に真上でハンガーから手を離すと,どうなるでしょうか?
「ハンガーが1回ゆれる時間」も考えてみてください.
※結果はちょっとおかしなことになりますが,実は正しいです.
このお話は,今度のショーの中でも出てきます.
その中に答えが出てくるので,ぜひ聞いてみてください!
今回はふりこの紹介でした.
当日は他にも色々な実験があります.
只今,鋭意準備中です.お楽しみに!