モデル化

こんにちは、計算機班です。

前回は計算機が物理でどう役立っているのかを見ていきました。

そこでは計算機の計算力でもって物理を紐解いていくということをお話ししましたが、「紐解くと言っても具体的にどんなことをするのか？」「じゃあ、頑張るのはコンピュータであって物理学者じゃないのかよ」とかいう某SNSの某ゴリラに襲いかかられそうな質問が生じるのが当然かと思いますので今回はその辺をお話ししようと思います。

長ったらしい説明の前に今回の話を一言で言うと「モデル化」です。

＜物理現象のモデル化＞

私たちの身の回りの物理現象は、様々な物理量が様々な物理法則のもとで変化した、または変化しないその結果です。したがって注目する物理量がどう変化するのか計算したい時に、どんな物理法則があるのかということを計算機に教えてあげないと計算機は計算を始められません。

とはいえ、たくさんある物理法則のうちで物理量の変化に影響を及ぼさない法則があることも事実で、こういった法則は無視してもよさそうですよね。無視したほうが計算量が減るので計算スピードが上がるので無視できるものは無視するのが賢明です。また、たくさんあるうちの物理法則の中には私たちがまだ知らない法則があるかもしれません。こういった法則に対しては、観測や理論から打ち出された法則の「候補」を使ってやるのが妥当です。

このように対象とする物理現象を、計算が収束するように単純化したり、「候補」を考えることを「モデル化」と言います。

単純化すればいいとは言いましたが、単純化にも限度があって、あまりに単純化しすぎると現実の物理を十分に再現できなくなってしまうのでどの程度までのモデル化が十分かつ必要か見極める必要があります。

また「候補」探しには、先行研究をよく知っておく必要があります。ある一つの「候補」での計算結果が、他の観測や理論と一致しないならその「候補」がハズレだったということで次の「候補」探しの手がかりにします。

物理現象のモデル化に物理学者の仕事の一つがあります。

あまりピンとこない人は具体的に重力のモデル化を考えてみましょう。

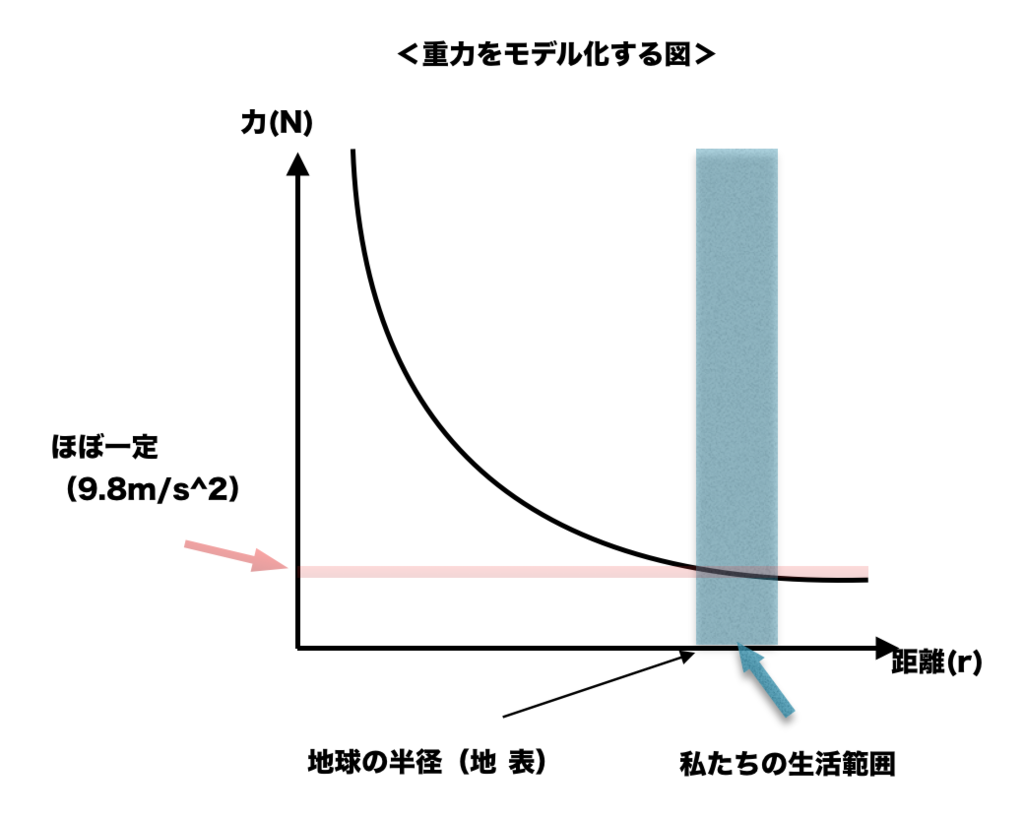
重力の大きさは、私たちが地球の中心から距離r離れたところにいた時にrの二乗に反比例します。

しかし実際地球に住んでいる限りは地球からそんなに遠く離れないので先ほどのrはほとんど地球の半径と見なせます、つまり受ける力の大きさは反比例せずほぼ一定です。これがご存知重力加速度g=9.8m/s^2ですね。

今のような「私たちの（垂直方向）移動範囲は地球の大きさに比べたら小さいから重力はほぼ一定とみなしていいでしょ」がモデル化です。

＜計算モデルの選択＞

物理現象のモデル化を先ほど話しましたが、計算物理学に於いては「計算モデル」を選ぶという、これまたエッセンシャルな仕事があります。

物理の方程式には微分がたくさん登場するのでひとまず微分を考えてみましょう。

計算機は数値計算をするので、私たちが扱う微分積分を差分和分に置き換えて計算します。

微分積分は差分和分の極限でありますが、ある微分積分に対応する差分和分は一意（一通り）ではありません。

具体的に言うと微分

に対応する差分は（代表的なもので）

が考えられます。これらだけを見ても3通り、さらにΔxの取り方には無限の取り方があります。

3通りの選び方によって計算結果はだいぶ変わってきます。Δxは元の微分を保ちたいのだから小さいほうが良さそうですが実は小さく取れば良いってものでもないのです。これらを選ぶにはどの差分和分が考えている物理現象に即した考え方になっているか、とか、たくさん計算した時に最終的に得られる計算結果が発散せず欲しい精度に収まるようなΔxはどれぐらいか、という考察をしてからプログラムしないとなりません。

たった一つの微分でもこれだけの考察があります。

実際に考えるのは、より高階の微分が含まれている微分方程式だったり、めちゃめちゃでかい行列計算だったりするので、欲しい精度や性質を保つように、適切な計算方法を選んでいく必要があります。

計算モデルの選択（既存の計算モデルで対応できなければ作るわけですが）に物理学者のもう一つの仕事があります。

だいぶ浅くモデル化を見ていきましたが、モデルの面白さは各モデルを深く掘り下げていったその先にあるので是非五月祭に足をお運びください。