第三の柱・計算機と物理

こんにちは

初めまして、計算機班です。

計算機班は計算機（コンピュータ）のちからを借りて物理現象を理解しようとすることを目標に活動している班です。

今回は計算機がどうやって物理学に役立つのか見ていきましょう。

例えば、引力について考えてみます。

高いところでリンゴを離すと下に落ちていきます。

これはニュートンが明らかにしたように、地球とリンゴの間に引力が働いた結果です。

引力は地球にもリンゴにも等価に働くので、リンゴと同じように、地球はリンゴに落ちていくという言い方もできます。

しかし地球はリンゴや私たちよりとても重いので地球が動いていないように見えるだけです。

ではここからは同じくらいの質量の物体の数を2個,3個,...と増やしていってみましょう。

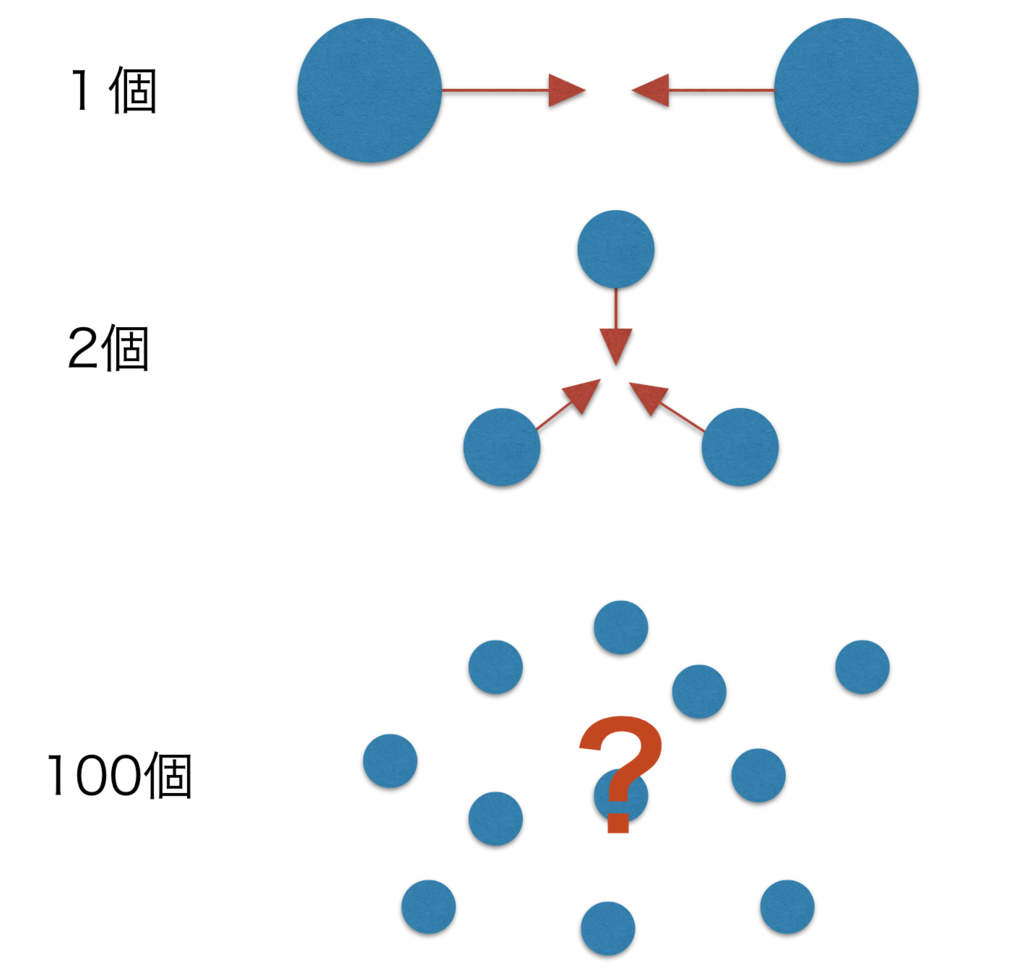
まずは物体が2個あった時。同じくらいの加速度で互いに近づいていきます。

高校では運動方程式を立てて動き方を計算し、実際に計算ができたと思います。

動き方が想像できますね。

次は物体が３個あった時。三角形状に配置されていれば重心あたりに近づいていきそうです。

詳しく「ここに近づく」とは言い切れませんが、なんとなく動き方が想像できそうですね。

では4個は、5個は…100個はどうなるでしょう。

もはや厳密に「ここに移動する」と言い切れないどころか大体の動き方さえ想像できません。

実際、優秀な物理学者でも100個の物体がある場合の動き方はわかりませし、

なんと、たった3個でも動き方を予測することはできないのです。

こういった時に計算機のちからを借りることになります。

計算機は繰り返し計算を素早く行うことが得意ですから、計算機に数値的に考えてもらうのです。

現実には物体がたくさんあって互いに引力、はたまた斥力を及ぼし合うという状況はたくさん考えられますから、こういった問題を考えることには非常に意味があることがわかると思います。

他にも計算機の活躍する場面はあります。

先のように計算機の力を借りたり、物理法則をたくさん見つけた後のことを考えてみましょう。

物理法則がたくさんわかったので、今度はこれらの法則を使って様々な現象を予測したくなります。

例えば一般相対性理論を作り上げたアインシュタインが重力波の存在を予測し、米国のレーザー干渉計型重力波検出器「LIGO」が2016年に重力波を直接観測したのは記憶に新しいです。

アインシュタインは方程式を解析的に（方程式を数値計算を使わず式変形して問題を考えることを「解析的」と言います。）計算して重力波の存在を予測できたわけですが、先の例のように物体がたくさんある系の動きだったり、様々な科学的現象が確率的に起こるような問題では解析的に取り組むことができなくなります。

こういった時に計算機を使って数値的に取り扱っていきます。

ではどんな問題も計算機で解いていけばいいではないかという声が聞こえてきそうですが、

解析解にはいいことがあって、現象の性質を如実に反映する結果を得られるので解析的に解ける場合は解析解を求めることが目標になります。

解析的に解けるのかわからない問題、部分的には解析的に解けるがある一部は解けないなどという場合には場合には計算機を使って、結果の性質を掴んでからそれをヒントに新しい現象の理解につながるということもあるので、方程式を計算機で解くことは非常に有効な手段であるのです。

2例説明しましたが、計算機が物理学では最高のアイテムであることがわかったと思います。

上の2例以外にも計算機が物理学で使われる場面はたくさんあり、計算機は理論・実験問わず幅広く使われているツールであるばかりか、第三の柱として計算物理学という分野があるほどです。

それだけ幅広く使われる計算機ですから、私たち計算機班では班員それぞれが興味の有る物理現象をテーマに取り上げて計算機を使ってアプローチしています。

Physics Lab.2017では五月祭までの研究成果を発表します。

計算機がどんな風に使われているのか、そしてその威力を是非体感しに来てください。